© Peter L Sørensen

GEOMETRI Vinkelsummen i en trekant er altid 180° Retvinklede trekanter (Der er formler nederst) Hvis den ene vinkel i en trekant er 90°, så kaldes trekanten retvinklet. En ret vinkel markeres ofte med et lille kvadrat. Siden over for den rette vinkel kaldes hypotenusen. De 2 andre sider kaldes kateter. 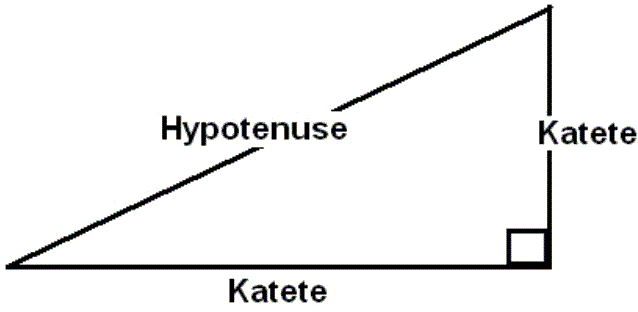Pythagoras' sætning Kvadratet på hypotenusen er lig summen af kateternes kvadrater. Her ses et eksempel. 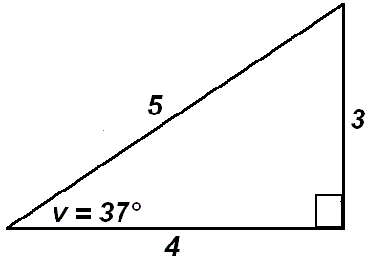Med udgangspunk i trekantvinklen v til venstre tales om den hosliggende katete, her forkortet hosl.k , som har længden 4 og den modstående katete, her forkortet modst, som har længden 3. Hypotenusen er her forkortet således: hyp. 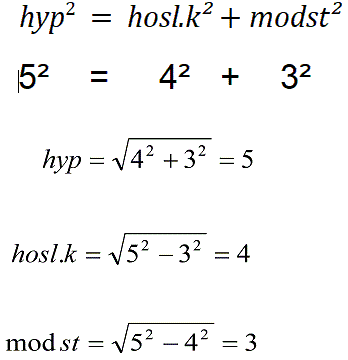Sinus, Cosinus og Tangens Her benyttes formuleringen spids vinkel, og det er en vinkel mellem 0° og 90° Hvis man kender 2 sider i en retvinklet trekant, kan man beregne de spidse vinkler ved at benytte Sinus, Cosinus og Tangens på en lommeregner eller kalkulator. Det er standard at benytte forkortelserne: Sin, Cos og Tan. Til enhver spids vinkel er knyttet et tal, vi kalder Sinus til vinklen. Også til Cosinus og Tangens er knyttet et tal til enhver spids vinkel og der gælder: Sinus til en spids vinkel i en retvinklet trekant er modstående katete divideret med hypotenusen. Cosinus til en spids vinkel i en retvinklet trekant er hosliggende katete divideret med hypotenusen Tangens til en spids vinkel i en retvinklet trekant er modstående katete divideret med hosliggende katete. Sammenhængen mellem sider og vinkler kan udtrykkes således: Sin v = modstående katete hypotenusen Cos v = hosliggende katete hypotenusen Tan v = modstående katete hosliggende katete Når man kender Sin, Cos eller Tan til en vinkel mellem 0° og 90°, så kan selve vinklen findes på en lommeregner eller kalkulator ved hjælp af Sin-1, Cos-1 eller Tan-1 . Eksempel: Find vinklen v i en retvinklet trekant, hvor Sin(v) = 0,5. v = Sin-1(0,5) = 60°. Formler: hyp² = hosl.k² + modst² hyp =   _____________ √hosl.k² + modst² hosl.k =   __________ √hyp² - modst² modst =   __________ √hyp² - hosl.k² Sin v = modst hyp   modst = hyp·Sin v hyp = modst Sin v Cos v = hosl.k hyp hosl.k = hyp·‭Cos v hyp = hosl.k cos v Tan v = modst hosl.k modst = hosl·Tan v hosl.k = modst Tan v Eksempler: hyp² = 4² + 3² = 5 hyp =   ______ √4² + 3²  = 5 hosl.k =   ______ √5² - 3²  = 4 modst =   ______ √5² - 4²  = 3 Sin v  =    3     5    =  0,6 v  =  Sin-1(0,6)  = 37° modst = 5·Sin(37°) = 3 hyp = 3 Sin(37°)  = 5 Cos v  =   4  5   =  0,8 hosl.k = 5·‭Cos(37°)=4 hyp = 4 cos(37°) Tan v =  3  4  0,75 modst = 4·Tan(35°)=3 hosl.k = 3 Tan(37°) = 4 Opgaver