Aktiver kalkulator (pop op)
Link til kalkulator
|
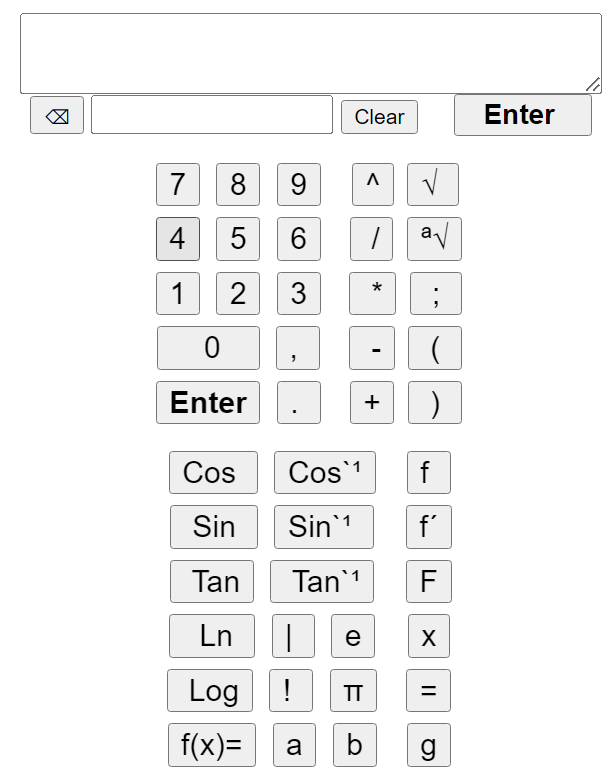
Vejledning til kalkulator
Aktiver kalkulator (pop op) Link til kalkulator
| 
|
| matematisk notation: |
|
Hvis du fortryder en indtastning, så tast ´Backspace`
eller klik i knappen: .
Både decimalkomma og decimalpunktum kan benyttes.
Tusind-punktum kan ikke benyttes.
Eventuelle vinkler skal anføres i grader.
| Skriv | Forklaring| Gange | fx: 7*3 i stedet for 7·3 | Division | fx: 1/2 i stedet for ½ | Potensopløfting: | fx: 5^2 i stedet for 5² | _ | √ Kvadratrod root(; Sqrt( KvRod( ^(1/2) ^0,5 _ | √9 kan fx skrives: root(;9) Husk semikolon ; Sqrt(9) , KvRod(9), 9^(1/2) eller 9^0,5 Tasten √ kan også benyttes Så skal du blot udfylde en skabelon og taste Enter. Hvis regneudtrykket er færdigt, skal du taste Enter igen. _ | ª√ a´te rod root( nrod( ^(1/a) ³√27 kan skrives: | root(3;27) Husk semikolon ; eller 27^(1/3) Tasten ª√ kan også benyttes. Så skal du blot udfylde en skabelon og taste Enter. Hvis regneudtrykket er færdigt, skal du taste Enter igen. π | PI() fx: 2*PI()*5 = 2·π·5 | e | Eulers tal = ca 2,7 e() fx: 2*e()*5 = 2·e·5 | Log | Almindelig logritme Log10 fx: Log(10) = Log10(10) = 1 | Naturlig | eksp.funktion exp fx: eksp(1) = exp(1) = e | og eksp(2) = exp(2) = e()^2 = e² Ln | Naturlig logaritme fx: Ln(eksp(7)) = 7 | Sin-1 | Omvendte til Sinus ArcSin Sin^-1 fx: ArcSin(1/2) = Sin^-1(1/2) = 30° | Vinkler er i grader Cos-1 | Omvendte til Cosinus ArcCos Cos^-1 fx: ArcCos(1/2) = Cos^-1(1/2) = 60° | Vinkler er i grader Tan-1 | Omvendte til Tangens ArcTan Tan^-1 fx: ArcTan(1) = Tan^-1(1) = 45° | Vinkler er i grader ! Fakultet | fx: 3! = 1·2·3 = 6 | | | Numerisk værdi fx: |-6| = 3 | a= | b= Tildeling af værdi b= Du kan gemme talværdier i | bogstaver. Skriv fx: a=2 og skriv senere 3a og du vil få resultatet 6. f(x)= | Definition af funktion g(x)= Det er også muligt at benytte | funktioner. Skriv fx: f(x)=3x og senere kan du fx skrive f(2)+1, som bliver lig 3·2+1 = 7. ( Når du definerer en funktion, vil i de fleste tilfælde automatisk også blive defineret yderligere en funktion, den såkaldt afledede funktion, der viser, hvor hurtigt den oprindelige funktion ændrer funktionsværdi. Den afledede fuktion markeres med et mærke efter funktionsnavnet, fx : f´ ) |